Bidder

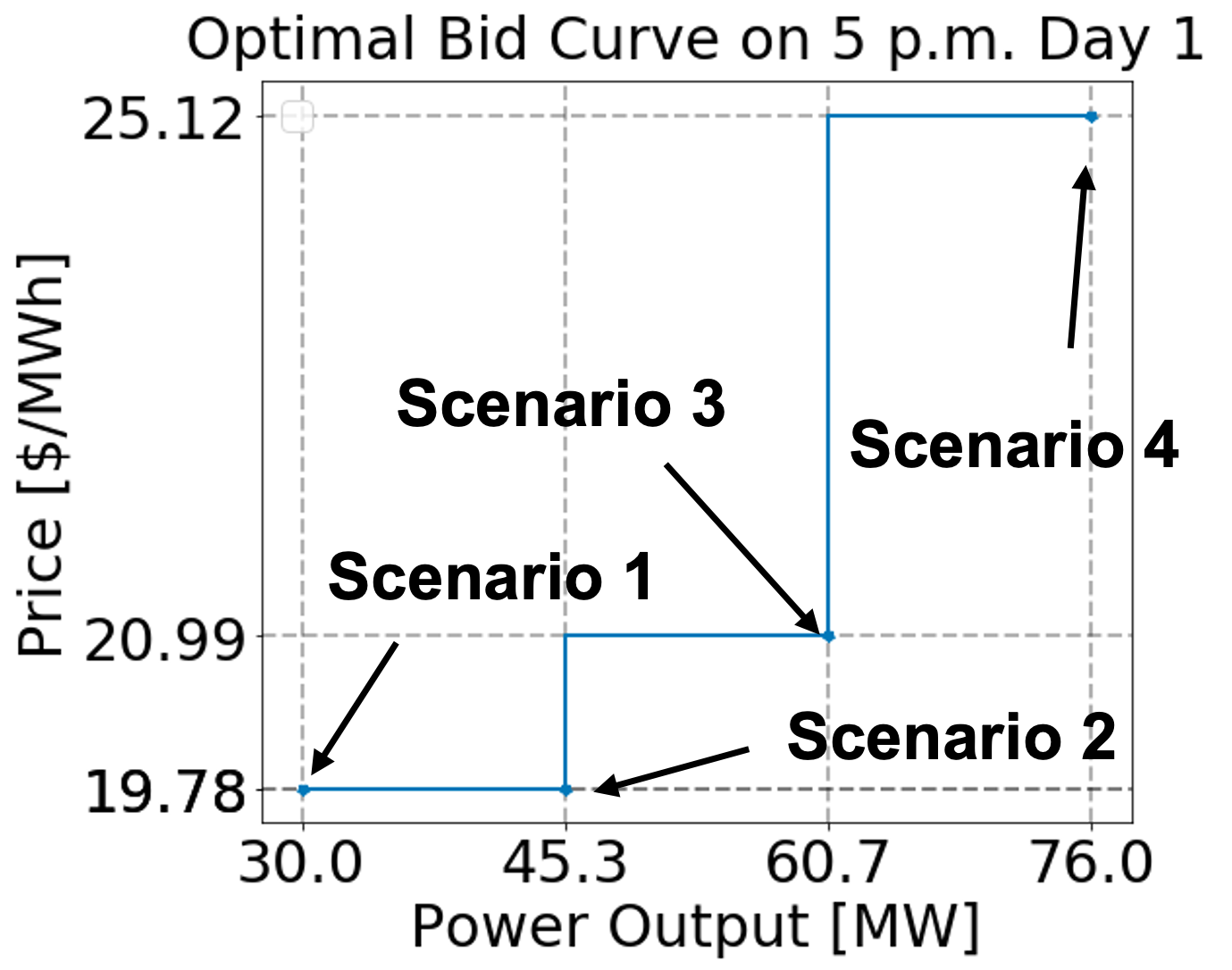
Market participating resources (e.g., generators, IESs) submit energy bids (a.k.a., bid curves) to the day-ahead and real-time markets for each trading time period to communicate their flexibility and marginal costs. As shown in the figure below, an energy bid is a piecewise constant function described by several energy offer price ($/MWh) and operating level (MW) pairs. Bid curves from each resource are inputs (i.e., parameters) in the market-clearing optimization problems solved by production cost models. Currently, the Bidder formulates a two-stage stochastic program to calculate the optimized time-varying bid curves for thermal generators. In this stochastic program, each uncertain price scenario has a corresponding power output. As shown in the figure, each of these uncertain price and power output pairs formulates a segment in the bidding curves.

class idaes.apps.grid_integration.bidder.Bidder(bidding_model_object, day_ahead_horizon, real_time_horizon, n_scenario, solver, forecaster, real_time_underbid_penalty=10000)

Wrap a model object to bid into the market using stochastic programming.

class idaes.apps.grid_integration.bidder.SelfScheduler(bidding_model_object, day_ahead_horizon, real_time_horizon, n_scenario, solver, forecaster, real_time_underbid_penalty=10000, fixed_to_schedule=False)

Wrap a model object to self schedule into the market using stochastic programming.